東京工業大学2023年大問1〔不等式の評価〕

この問題のレベル
| 思考力 | (3.0) |
| 知識力 | (4.0) |
| 計算力 | (2.0) |
| 総合難易度 | (3.0) |
\(\displaystyle\int_{0}^{2023}\frac{1}{x+e^x}dx\)の整数部分を求めよ.

まずは方針をたてよう!
・\(\displaystyle\frac{1}{x+e^x}\)を不等式で挟んで(評価して)積分しようのかな?
・\(\displaystyle e^x≧x+1\)を利用してみようかな?
・類題:大阪大学 (2014)があった
【解答】



まず\(\displaystyle e^x≧x+1\)を使いたいので示します
すべての実数\(\displaystyle x\)について,不等式\(\displaystyle e^x≧x+1\)を示す.
\(\displaystyle f(x)=e^x-(x+1)\)とおくと
\(\displaystyle f’(x)=e^x-1\)
\(\displaystyle f’(x)=0\)とすると\(\displaystyle x=0\)
\(\displaystyle f(x)\)の増減表は以下になる.
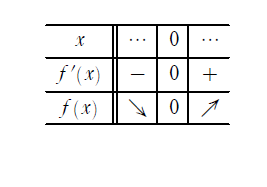

よって\(\displaystyle f(x)\)は\(\displaystyle x=0\)のとき最小値\(\displaystyle 0\)をとる.
したがって,すべての実数\(\displaystyle x\)について\(\displaystyle f(x)≧0\)
よって\(\displaystyle e^x≧x+1\)



これで\(\displaystyle e^x≧x+1\)が使えます!
次に
\(\displaystyle x+1≦e^{x}\)より\(\displaystyle x≧0\)において
\(\displaystyle 0≦x+1≦e^{x}\)



いま積分区間が
\(\displaystyle 0から2023\)より\(\displaystyle x≧0\)になります
\(\displaystyle 0≦x≦e^{x}-1\) (∴\(\displaystyle x≧0\))
\(\displaystyle e^{x}≦e^{x}+x≦2e^{x}-1\) (∴すべての辺に\(\displaystyle +e^{x}\))
\(\displaystyle \frac{1}{2e^{x}-1}≦\frac{1}{x+e^x}≦\frac{1}{e^x}\)
\(\displaystyle \frac{2}{2e^{x}-1}≦\frac{2}{x+e^x}≦\frac{2}{e^x}\)
\(\displaystyle \int_{0}^{2023}\frac{2}{2e^{x}-1}dx≦\int_{0}^{2023}\frac{2}{x+e^x}dx≦\int_{0}^{2023}\frac{2}{e^x}dx\)
(画面サイズによって式がスワイプできます↑)



あとは
\(\displaystyle \int_{0}^{2023}\frac{2}{2e^{x}-1}dxと\int_{0}^{2023}\frac{2}{e^x}dx\)を計算してきます
\(\displaystyle \int_{0}^{2023}\frac{2}{e^x}dx\)
\(\displaystyle =\left[-2e^{-x}\right]^{2023}_0\)
\(\displaystyle =2(1-\frac{1}{e^{2023}})<2\)
よって\(\displaystyle \int_{0}^{2023}\frac{2}{e^x}dx<2\)・・・①



上から『2』で押さえられた時点で,\(\displaystyle\int_{0}^{2023}\frac{1}{x+e^x}dx\)は正になることから,下からは『0』か『1』で押さえられると予想できます!すなわち答えは,『0』か『1』になりそうです。
\(\displaystyle \int_{0}^{2023}\frac{2}{2e^{x}-1}dx\)
\(\displaystyle =2\int_{0}^{2023}\frac{e^{-1}}{2-e^{-1}}dx\)
\(\displaystyle =2\left[\log|2-e^{-x}|\right]^{2023}_0\)
\(\displaystyle =2\log(2-e^{-2023})\)
\(\displaystyle =\log(2-e^{-2023})^2\)
\(\displaystyle =\log(4-4e^{-2023}+e^{-4046})\)
\(\displaystyle >\log(4-4\frac{1}{4}+0)=\log3>1\)
よって\(\displaystyle \int_{0}^{2023}\frac{2}{2e^{x}-1}dx>1\)・・・②
①,②より
\(\displaystyle 1<\int_{0}^{2023}\frac{1}{x+e^x}dx<2\)
すなわち
\(\displaystyle \int_{0}^{2023}\frac{1}{x+e^x}dx\)の整数部分は 1 ■
〔不等式を評価して積分〕するという,難関大学では頻出の内容です。演習をしておきましょう!
類題:大阪大学(2014年)