この問題のレベル
| 思考力 | (4.0) |
| 知識力 | (3.0) |
| 計算力 | (3.0) |
| 総合難易度 | (3.0) |
\(\displaystyle a>0\)とする. 曲線 \(\displaystyle y=e^{-x^{2}}\)と\(\displaystyle x軸,y軸\),および直線 \(\displaystyle x=a\)で囲まれた図形を,\(\displaystyle y\)軸のまわりに1回転してできる回転体を \(\displaystyle A\)とする.
(1) \(\displaystyle A\)の体積 \(\displaystyle V\)を求めよ.
(2) 点 \(\displaystyle (t,0)\) \(\displaystyle (-a≦t≦a)\)を通り \(\displaystyle x\)軸と垂直なへ面による \(\displaystyle A\)の切り口の面積を \(\displaystyle S(t)\) とするとき,
不等式 \(\displaystyle S(t)≦\int^{a}_{-a}e^{-(s^{2}+t^{2})}ds\)を示せ.
(3) 不等式\(\displaystyle \sqrt{\pi(1-e^{-a^{2}})}≦\int^{a}_{-a}e^{-x^{2}}dx\)を示せ.
① \(\displaystyle A\)の方程式を作ろう!
② \(\displaystyle x=t\) で切って,積分しよう
【解答】
(1)
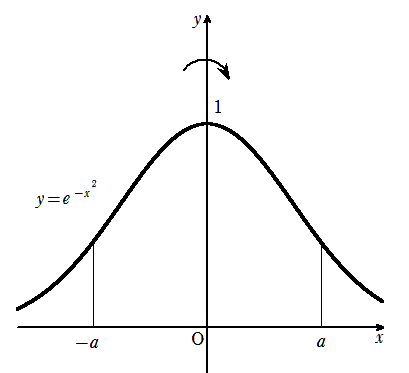
バームクーヘン積分より
\(\displaystyle V=\int^{a}_{0}2{\pi}xe^{-x^{2}}dx\)
\(\displaystyle =\pi\int^{a}_{0}-(-x^{2})^{\prime}e^{-x^{2}}dx\)
\(\displaystyle =-\pi\left[e^{-x^{2}}\right]^{a}_{0}\)
\(\displaystyle =\pi(1-e^{-a^{2}}) \) ■
(2)
\(\displaystyle y=e^{-x^{2}}\)
\(\displaystyle \log{y}=-x^{2}\)
\(\displaystyle x=\pm\sqrt{-\log{y}}\)
ここで \(\displaystyle y=u\)のとき
\(\displaystyle z\)軸上から \(\displaystyle xy\)平面をみると
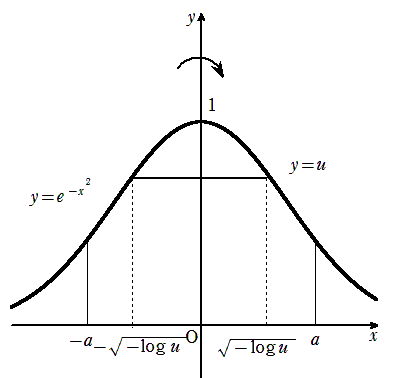
\(\displaystyle y\)軸上から \(\displaystyle xz\)平面をみると
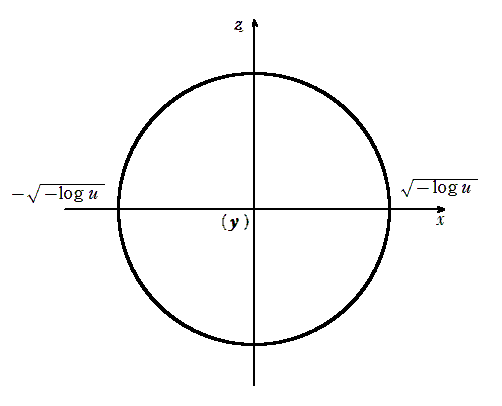
\(\displaystyle x^{2}+z^{2}≦-\log{u}\), \(\displaystyle y=u\)より
\(\displaystyle y\)軸まわりに回転してできる立体の方程式は
\(\displaystyle x^{2}+z^{2}≦-\log{y}\) ・・・①
直線\(\displaystyle x=a\)を\(\displaystyle y\)軸のまわるに回転してできる円柱面で囲まれた立体の方程式
\(\displaystyle x^{2}+z^{2}≦a^{2}\)・・・②
すなわち \(\displaystyle A\)の方程式は①かつ②
①かつ②を\(\displaystyle x=t\)できる
\(\displaystyle t^{2}+z^{2}≦-\log{y}\)
\(\displaystyle t^{2}+z^{2}≦a^{2}\)
よって
\(\displaystyle y≦-e^{-(t^{2}+z^{2})}\)
\(\displaystyle |z|≦\sqrt{a^{2}-t^{2}}\)
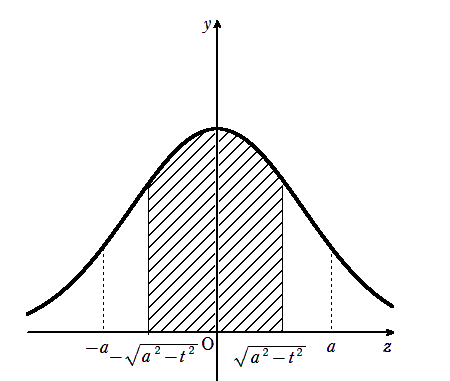
よって切り口の面積(上の図の斜線部の面積)は
\(\displaystyle S(t)=\int^{\sqrt{a^{2}-t^{2}}}_{-\sqrt{a^{2}-t^{2}}}e^{-(t^{2}+z^{2})}dz\)
\(\displaystyle ≦\int^{a}_{-a}e^{-(t^{2}+z^{2})}dz\)

\(\displaystyle z \)を\(\displaystyle s\)に変えても ,定積分の値は同じです。だから,文字を\(\displaystyle s\) に置き換えます
\(\displaystyle =\int^{a}_{-a}e^{-(s^{2}+t^{2})}ds\) ■
(3)
\(\displaystyle S(t)≦\int^{a}_{-a}e^{-(s^{2}+t^{2})}ds\)
\(\displaystyle =e^{-t^{2}}\times\int^{a}_{-a}e^{-s^{2}}ds\)
よって
\(\displaystyle int^{a}_{-a}S(t)dt\)
\(\displaystyle ≦\int^{a}_{-a}e^{-t^{2}}dt\times\int^{a}_{-a}e^{-s^{2}}ds\)



上の2つの積分の積は同じ値同士の掛け合わせです。だから1つにまとめることができます!
\(\displaystyle =(\int^{a}_{-a}e^{-x^{2}}dt)^{2}\)
(1)より
\(\displaystyle \pi(1-e^{-a^{2}})≦(\int^{a}_{-a}e^{-x^{2}}dt)^{2} \)
よって
\(\displaystyle \sqrt{\pi(1-e^{-a^{2}})}≦\int^{a}_{-a}e^{-x^{2}}dx\) ■