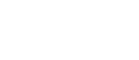一橋大学2014年〔整数問題〕

| 思考力 | (2.5) |
| 知識力 | (3.0) |
| 計算力 | (2.0) |
| 総合難易度 | (3.0) |
\(\displaystyle a-b-8\) と \(\displaystyle b-c-8\)が素数となるような素数の組 \(\displaystyle (a, b, c )\) をすべて求めよ.

この問題を解くのに必要な知識が3つあります。これらは当たり前のようですが,重要な知識になります!



さらに,この問題は2005年の一橋大学〔整数問題〕と同じ知識をつかいます!
【1つ目】
最小の素数は \(\displaystyle 2\) である.
【2つ目】
偶数の素数は \(\displaystyle 2\) のみで,他の素数は奇数である.
【3つ目】
\(\displaystyle 3\) より大きい素数は \(\displaystyle 3\) の倍数でない.
※この問題では使わないが当然,5より大きい素数は5の倍数でないし,7より大きい素数は7の倍数ではない
・\(\displaystyle a, b, c\) が偶数か奇数かを調べる
・偶数か奇数かがわかれば
\(\displaystyle a-b-8\) と \(\displaystyle b-c-8\)が偶数か奇数かがわかる
【解答】
\(\displaystyle a-b-8\) と \(\displaystyle b-c-8\) は素数より
\(\displaystyle a-b-8≧2\) , \(\displaystyle b-c-8≧2\)



最小の素数は \(\displaystyle 2\)だよ
\(\displaystyle a-b-8≧0\) , \(\displaystyle b-c-8≧0\)
素数と言われているから,\(\displaystyle 0\)以上で立式するのは間違えです
\(\displaystyle a≧b+10\) , \(\displaystyle b≧c+10\)・・・①
ここで,\(\displaystyle b≧2\) , \(\displaystyle c≧2\)より
①の不等式は
\(\displaystyle a≧b+10≧12\) , \(\displaystyle b≧c+10≧12\)となる
よって \(\displaystyle a, b\) は奇数



偶数の素数は \(\displaystyle 2\)のみ.したがって, \(\displaystyle a≧12\) , \(\displaystyle b≧12\)とわかれば,\(\displaystyle a, b\)が \(\displaystyle 2\)でないことがわかり奇数だとわかる
すなわち \(\displaystyle a-b-8\) は偶数
∴ \(\displaystyle a-b-8=2\)
∴ \(\displaystyle a=b+2\)・・・②
次に, \(\displaystyle b-c-8=p\) \(\displaystyle (p:素数)\)とおく
∴ \(\displaystyle p+c=b-8\) ・・・③



\(\displaystyle p+c\) と\(\displaystyle b-8\) に分けた理由を説明します.
それは \(\displaystyle b\) は奇数だとわかっている為\(\displaystyle b-8\) も奇数だとわかるからです.
それに対して \(\displaystyle c\) は偶数か奇数か不明なために \(\displaystyle p+c\) が偶数か奇数か不明です.
すなわち,(不明な文字)=(奇数だとわかる文字)で分けたのです.
③の右辺は, \(\displaystyle b\) が奇数より\(\displaystyle b-8\)も奇数
すなわち
③の左辺 \(\displaystyle p+c\) も奇数となるので,
\(\displaystyle p, c\) のどちらかは偶数でもう一方は奇数である.



\(\displaystyle p\) と \(\displaystyle c\) は素数であるため,偶数であれば \(\displaystyle 2\)に決まります
(ア)\(\displaystyle c=2\)のとき
③より \(\displaystyle b=p+10\)
②より \(\displaystyle a=b+10=p+20\)
(ⅰ) \(\displaystyle p=3\) のとき
\(\displaystyle a=23, b=13\) となり
\(\displaystyle (a, b, c )=(23, 13, 2)\) となり適している



これで解答終了ではなく, 他に適する解がない(もしくはある)ことを記述すること!
(ⅱ) \(\displaystyle p≧5\) のとき
\(\displaystyle p\) は素数より \(\displaystyle 5\)以上の素数で \(\displaystyle 3\)の倍数はない.
したがって, \(\displaystyle p=3k+1\), \(\displaystyle p=3k+2\)とおける( \(\displaystyle k:自然数\))



\(\displaystyle 3\) より大きい素数は \(\displaystyle 3\) の倍数でない
\(\displaystyle p=3k+1\)とすると,
\(\displaystyle a=p+20=3(k+7)\)となり
\(\displaystyle a が 3 より大きい 3 の倍数\)となり素数にはなり得ない
∴不適
\(\displaystyle p=3k+2\) とすると,
\(\displaystyle b=p+10=3(k+4)\)となり
\(\displaystyle bが3より大きい3の倍数\)となり素数にはなり得ない
∴不適
以上より\(\displaystyle p≧5\)で\(\displaystyle (a, b, c )\)は素数にならない
(イ)\(\displaystyle p=2\)のとき
(ア)のときの\(\displaystyle pとc\)の文字を入れ替えただけなので
(ア)と同様にして\(\displaystyle c=3\)
∴\(\displaystyle (a, b, c )=(23, 13, 3)\)
以上(ア),(イ)より
∴\(\displaystyle (a, b, c )=(23,13,2),(23, 13, 3)\) ■
・最小の素数は \(\displaystyle 2\) であることから不等式を作る
・偶数の素数は \(\displaystyle 2\) のみ
・\(\displaystyle 3\) より大きい素数は \(\displaystyle 3\) の倍数でない
・他に答えがないということも示す