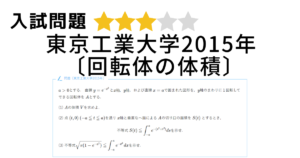
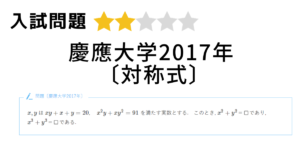
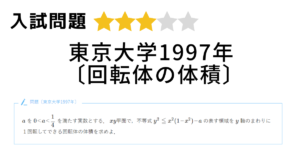
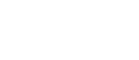大阪大学2014年〔区分求積法〕

この問題のレベル
| 思考力 | (2.5) |
| 知識力 | (3.0) |
| 計算力 | (2.0) |
| 総合難易度 | (3.0) |
\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)の整数部分を求めよ.

東京工業大学2023年にも「~の整数部分を求めよ」が出題されています
方針①
\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)を不等式で挟めるか考えよう.
挟むことができれば,例えば
\(\displaystyle 1<\sum_{n=1}^{4000}\frac{1}{\sqrt{n}}<2\)だとすると
\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)の整数部分は1だと分かる!
方針②
\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)から区分求積法を連想させよう.
区分求積法は【下からの評価】と【上からの評価】ができた!
これを利用して,①を達成させる!
【解答】
(ア) 下から評価する.
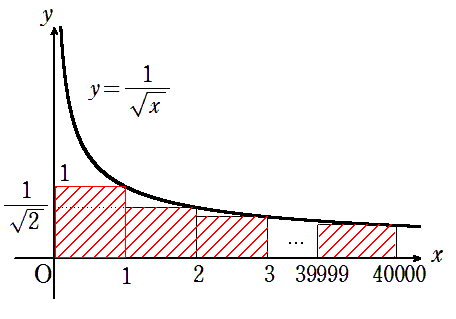

\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}=1+\frac{1}{\sqrt{2}}+\dotsb+\frac{1}{\sqrt{4000}}\)
は上図の斜線部の面積に等しい.
よって図より
\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}<1+\int_1^{4000}\frac{1}{\sqrt{x}}dx\)
\(\displaystyle =1+\left[2x^{\frac{1}{2}}\right]^{4000}_1\)
\(\displaystyle =1+2\lbrace (200^2)^{\frac{1}{2}}-1\rbrace\)
\(\displaystyle =400-1\)
\(\displaystyle =399 \)
∴\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}<399 \)
(イ) 上から評価する.
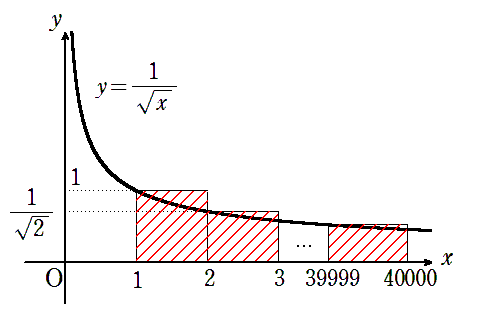

\(\displaystyle \sum_{n=1}^{3999}\frac{1}{\sqrt{n}}=1+\frac{1}{\sqrt{2}}+\dotsb+\frac{1}{\sqrt{3999}}\)
は上図の斜線部の面積に等しい.
よって図より
\(\displaystyle \int_1^{4000}\frac{1}{\sqrt{x}}dx<\sum_{n=1}^{3999}\frac{1}{\sqrt{n}}\)



(ア)の結果から計算せずとも左辺は\(\displaystyle 398\)
\(\displaystyle 398<\sum_{n=1}^{4000}\frac{1}{\sqrt{n}}-\frac{1}{\sqrt {4000}}\)



(ア)の結果とまとめたいから\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)をわざと作ったよ!そのつじつまを合わせるために\(\displaystyle \frac{1}{\sqrt {4000}}\)を引いたんだ
\(\displaystyle 398+\frac{1}{\sqrt {4000}}<\sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)
∴\(\displaystyle 398+\frac{1}{200}<\sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)
以上(ア)(イ)より
\(\displaystyle 398+\frac{1}{200}<\sum_{n=1}^{4000}\frac{1}{\sqrt{n}}<399\)
すなわち
\(\displaystyle \sum_{n=1}^{4000}\frac{1}{\sqrt{n}}\)の整数部分は\(\displaystyle 398\)■