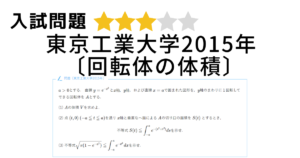
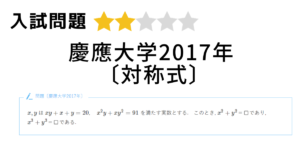
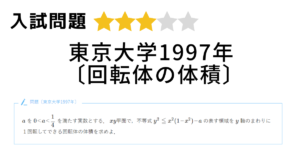
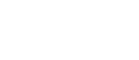[数Ⅲ]基本の不定積分 その1

問題 [目標15分]
次の不定積分を求めよ.
(1) \(\displaystyle\int x^{-4}dx\)
(2) \(\displaystyle\int\frac{1}{x^{3}}dx\)
(3) \(\displaystyle\int\sqrt{x^{3}}dx\)
(4) \(\displaystyle\int\frac{1}{3\sqrt{x}}dx\)
(5) \(\displaystyle\int 3x^{-3}dx\)
(6) \(\displaystyle\int \sqrt[4]{x^{3}}dx\)
(7) \(\displaystyle\int x^{2}\sqrt{x}dx\)
(8) \(\displaystyle\int \sqrt{x}(x-1)dx\)
(9) \(\displaystyle\int(4x^{\frac{1}{3}}+3x^{\frac{1}{2}}-1)dx\)
(10) \(\displaystyle\int \frac{2x^{3}+x^{2}}{x}dx\)
(11) \(\displaystyle\int \frac{x+1}{x}dx\)
(12) \(\displaystyle\int\frac{3x^{2}+5x}{x^{2}}dx\)
(13) \(\displaystyle\int \frac{2x}{\sqrt{x}}dx\)
(14) \(\displaystyle\int\frac{dx}{\sqrt[3]{x}}\)
(15) \(\displaystyle\int \frac{2x-1}{\sqrt{x}}dx\)
POINT
① \(\displaystyle\int x^{n}dx=\frac{1}{n+1}x^{n+1}+C (n\ne-1)\)
② \(\displaystyle\int \frac{1}{x}dx=\log|x|+C\)

まずは\(\displaystyle\int x^{n}dx\)の形に直してから計算すること
【解答】\(C\) は積分定数
(1) \(\displaystyle\int x^{-4}dx=-\frac{1}{3}x^{-3}+C\)
(2) \(\displaystyle\int\frac{1}{x^{3}}dx\)
\(\displaystyle=\int{x^{-3}}dx\)
\(\displaystyle=-\frac{1}{2}x^{-2}+C\)
(3) \(\displaystyle\int\sqrt{x^{3}}dx\)
\(\displaystyle=\int x^{\frac{3}{2}}dx\)
\(\displaystyle=\frac{2}{5}x^{\frac{5}{2}}+C\)
(4) \(\displaystyle\int\frac{1}{3\sqrt{x}}dx\)
\(\displaystyle=\int\frac{1}{3}x^{-\frac{1}{2}}dx\)
\(\displaystyle=\frac{2}{3}x^{\frac{1}{2}}+C\)
(5) \(\displaystyle\int 3x^{-3}dx=-\frac{3}{2}x^{-2}+C\)
(6) \(\displaystyle\int \sqrt[4]{x^{3}}dx\)
\(\displaystyle=\int x^{\frac{3}{4}}dx\)
\(\displaystyle=\frac{4}{7}x^{\frac{7}{4}}+C\)
(7) \(\displaystyle\int x^{2}\sqrt{x}dx\)
\(\displaystyle=\int x^{\frac{5}{2}}dx\)
\(\displaystyle=\frac{2}{7}x^{\frac{7}{2}}+C\)
(8) \(\displaystyle\int \sqrt{x}(x-1)dx\)
\(\displaystyle=\int (x^{\frac{3}{2}}-x^{\frac{1}{2}})dx\)
\(\displaystyle=\frac{2}{5}x^{\frac{5}{2}}-\frac{2}{3}x^{\frac{3}{2}}+C\)
(9) \(\displaystyle\int(4x^{\frac{1}{3}}+3x^{\frac{1}{2}}-1)dx=3x^{\frac{4}{3}}+2x^{\frac{3}{2}}-x+C\)



(10)から分数関数になります.
分数関数であっても割り算をして\(\displaystyle\int x^{n}dx\)の形に直してから計算しよう
(10) \(\displaystyle\int \frac{2x^{3}+x^{2}}{x}dx\)
\(\displaystyle=\int (2x^{2}+x)\)
\(\displaystyle=\frac{2}{3}x^{3}+\frac{1}{2}x^{2}+C\)
(11) \(\displaystyle\int \frac{x+1}{x}dx\)
\(\displaystyle=\int (1+x^{-1})dx\)
\(\displaystyle=x+\log|x|+C\)
(12) \(\displaystyle\int\frac{3x^{2}+5x}{x^{2}}dx\)
\(\displaystyle=\int (3+5x^{-1})dx\)
\(\displaystyle=3x+5\log|x|+C\)
(13) \(\displaystyle\int \frac{2x}{\sqrt{x}}dx\)
\(\displaystyle=\int 2x^{\frac{1}{2}}dx\)
\(\displaystyle=\frac{4}{3}x^{\frac{3}{2}}+C\)
(14) \(\displaystyle\int\frac{dx}{\sqrt[3]{x}}\)
\(\displaystyle=\int x^{-\frac{1}{3}}dx\)
\(\displaystyle=\frac{3}{2}x^{\frac{2}{3}}+C\)
(15) \(\displaystyle\int \frac{2x-1}{\sqrt{x}}dx\)
\(\displaystyle =2・\frac{2}{3}x^{\frac{3}{2}}-2x^{\frac{1}{2}}+C\)
\(\displaystyle =\frac{4}{3}x^{\frac{3}{2}}-2x^{\frac{1}{2}}+C\)