東京工業大学2023年大問4〔立体の体積〕

この問題のレベル
| 思考力 | (4.0) |
| 知識力 | (3.5) |
| 計算力 | (4.0) |
| 総合難易度 | (4.0) |
\(\displaystyle xyz\)空間において,\(\displaystyle x\)軸を軸とする半径\(\displaystyle 2\)の円柱から\(\displaystyle |y|<1\)かつ\(\displaystyle |z|<1\)で表される角柱の内部を取り除いたものを\(\displaystyle A\)とする.また,\(\displaystyle A\)を\(\displaystyle x\)軸のまわりに\(\displaystyle 45°\)回転してから\(\displaystyle z\)軸のまわりに\(\displaystyle 90°\)回転したものを\(\displaystyle B\)とする.\(\displaystyle A,B\)の共通部分の体積を求めよ.
【解答】
立体\(\displaystyle A\)について,\(\displaystyle z=t\)で切断して,
立体\(\displaystyle A\)を\(\displaystyle x\)軸からみると下図になる.
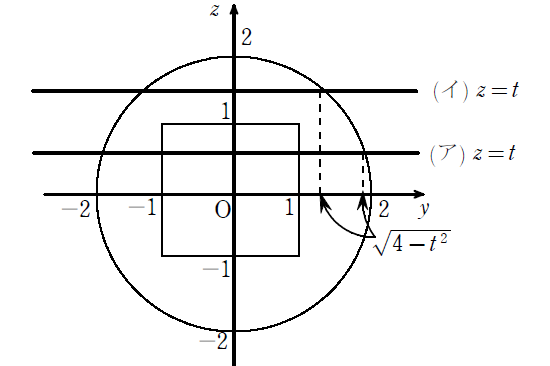
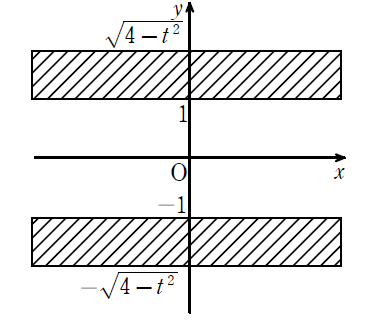
(ア)\(\displaystyle 0≦t≦1\)のとき
(イ)\(\displaystyle 1≦t≦2\)のとき
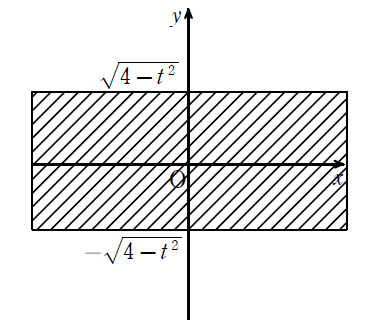
次に,立体\(\displaystyle B\)について,\(\displaystyle z=t\)で切断して,
立体\(\displaystyle B\)を\(\displaystyle y\)軸からみると下図になる.
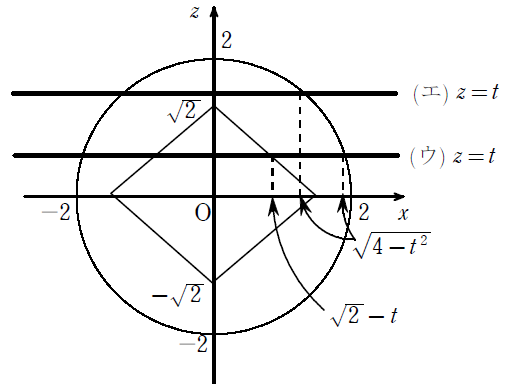
(ウ)\(\displaystyle 0≦t≦\sqrt{2}\)のとき
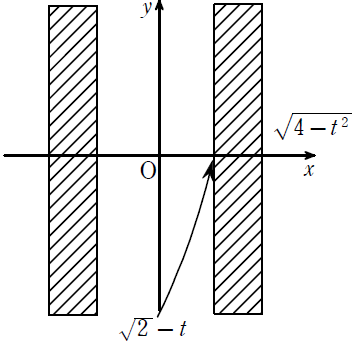
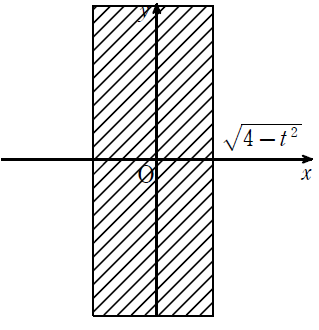
(エ)\(\displaystyle \sqrt{2}≦t≦2\)のとき
対称性より\(\displaystyle x≧0,y≧0\)の共通部分の免責を\(\displaystyle S(t)\)として
[1]\(\displaystyle 0≦t≦1\)のとき
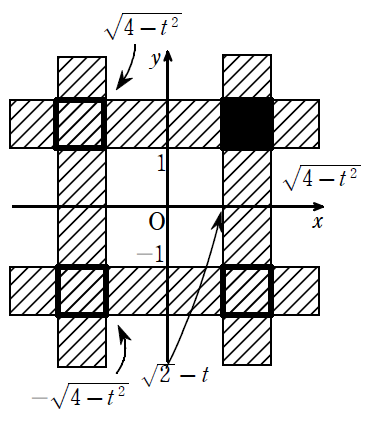
\(\displaystyle \frac{S(t)}{4}=(\sqrt{4-t^2}-\sqrt{2}+1)(\sqrt{4-t^2}-1)\)
\(\displaystyle =-t^2+4+\sqrt{2}-t+t\sqrt{4-t^2}-(\sqrt{2}+1)\sqrt{4-t^2}・・・①\)
(画面サイズによって式がスワイプできます↑)
[2]\(\displaystyle 1≦t≦\sqrt{2}\)のとき
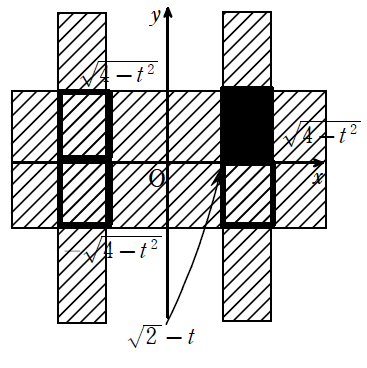
\(\displaystyle \frac{S(t)}{4}=(\sqrt{4-t^2}-\sqrt{2}+1)(\sqrt{4-t^2})\)
\(\displaystyle =-t^2+4+t\sqrt{4-t^2}-\sqrt{2}\sqrt{4-t^2}・・・②\)
[3]\(\displaystyle \sqrt{2}≦t≦2\)のとき
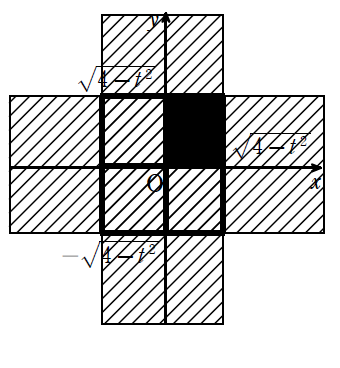
\(\displaystyle \frac{S(t)}{4}=(\sqrt{4-t^2})^2\)
\(\displaystyle =-t^2+4・・・③\)
以上,[1]から[3]より
求める体積を\(\displaystyle V\)とすると対称性より
\(\displaystyle V=2\int_{0}^{2}S(t)dt\)から
\(\displaystyle \frac{V}{8}=\int_{0}^{1}(①式)dt+\int_{1}^{\sqrt{2}}(②式)dt+\int_{\sqrt{2}}^{2}(③式)dt\)
(画面サイズによって式がスワイプできます↑)
\(\displaystyle \vdots\)
計算省力(後日更新予定)
∴\(\displaystyle V=60-4\sqrt{3}-\frac{4}{3}\pi(3\sqrt{2}+2)-\frac{16\sqrt{2}}{3}\) ■